
The n effciency gures are valid for n Biot number 0.25, i.e., Bi f ¼ h(t2) k 0:25 (17:6) Barkwill et al.(3) recently converted the graphical results presented in Figure 17.3 into. Note that the fin surface area that should be used with this fin efficiency is: area, A p, and the surface area, A f, in terms of the n length, L, n thickness at the base, t, and the n width, w, for various n types. The function then calls a corresponding non-dimensional function, which determines the fin efficiency in terms of the fin parameter mL, described below.

Typically, the fin material has a high thermal conductivity.
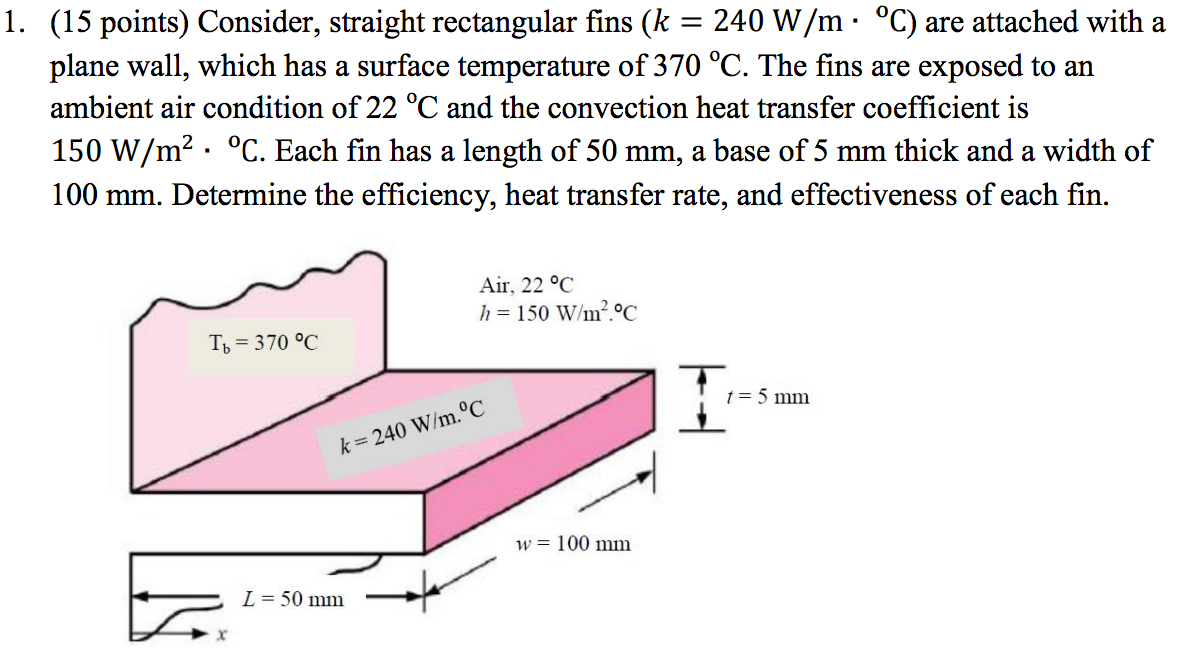
To account for the convection from the tip, the function will use a corrected length where: Fins are used in a large number of applications to increase the heat transfer from surfaces. The rectangular prisms width is 10 inches. This function is applicable for a fin where W>th (i.e., the fin is infinitely long into the page). Divide the volume by the product of the length and height to calculate the rectangular prisms width. To find surface area for a rectangular prism, use the formula SA 2ab + 2bc + 2ac, where a is the width, b is the height, and c is the length. This is how the human body surface area was calculated as well: subject's bodies were covered in stripes of paraffin, which were then removed, sliced and measured.Dimensional: eta_fin_straight_rect(th, L, h, k)įunction eta_fin_straight_rect calculates the fin efficiency of a straight fin with a rectangular base. Irregularly shaped areas are often divided into several rectangles when one needs to calculate their area, but can't do a precise calculation. Ideally, the size of the fin tube surface area of your heat exchange is directly proportional to the demand for heat transfer required. Practical applicationsĪrea of a rectangle calculations have a vast array of practical applications: construction, landscaping, internal decoration, architecture, engineering, physics, and so on and so forth. We can also label the length (l), width (w), and height (h) of the prism and use the formula, SA2lw+2lh+2hw, to find the surface area. To find the surface area of a cuboid, add the areas of all 6 faces. Since in multiplication the order in which the numbers are multiplied does not matter, you need not worry about switching the places of the two measurements. Surface area is the sum of the areas of all faces (or surfaces) on a 3D shape. Fig.3 Rectangular fin attached to cylinder Heat lost by fin.
Triangular fins are attractive, since for an equal heat transfer it requires much less volume than rectangular fin. FIN Rectangular Fin: The rectangular fin as shown in Fig.3 with L as the length of the fin, as thickness of the fin and W width of fin and assuming the heat flow is unidirectional and it is along length and the heat transfer coefficient (h) on the surface of the fin is constant. A rectangular bedroom with one wall being 15 feet long and the other being 12 feet long is simply 12 x 15 = 180 square feet. Rectangular fin and triangular fins are straight fins. Thus, the area is 2r + 2rh (as the length of the rectangle is the circumference of the circles). All analyses were performed for fins of rectangular cross section. For example, a garden shaped as a rectangle with a length of 10 yards and width of 3 yards has an area of 10 x 3 = 30 square yards. The area of a rectangle is L x W (Length x Width). Compared to base area of the rectangular fins, the cylindrical fins will have an unfinned area of tw 4D2/4 0.000205 m2 4(19.635x10-6 m2) 0. opening angles between adjacent fins and various values of surface emissivity. The area of any rectangular place is or surface is its length multiplied by its width.


 0 kommentar(er)
0 kommentar(er)
